x

实数系几大基本定理
科学原理
2026-01-07
菜科探索
+
登录后畅享更多功能

实数系的基本定理也称实数系的完备性定理、实数系的连续性定理,这些定理分别是确界存在定理、单调有界定理、有限覆盖定理、聚点定理、致密性定理、闭区间套定理和柯西收敛准则,共7个定理,。

一、上(下)确界原理
非空有上(下)界数集必有上(下)确界。
二、单调有界定理
单调有界数列必有极限。
具体来说:
单调增(减)有上(下)界数列必收敛。
三、闭区间套定理(柯西-康托尔定理)
对于任何闭区间套,必存在属于所有闭区间的公共点。
若区间长度趋于零,则该点是唯一公共点。

四、有限覆盖定理(博雷尔-勒贝格定理,海涅-波雷尔定理)
闭区间上的任意开覆盖,必有有限子覆盖。
或者说:闭区间上的任意一个开覆盖,必可从中取出有限个开区间来覆盖这个闭区间。
五、极限点定理(波尔查诺-魏尔斯特拉斯定理、聚点定理)
有界无限点集必有聚点。
或者说:每个无穷有界集至少有一个极限点。
六、有界闭区间的序列紧性(致密性定理)
有界数列必有收敛子列。
七、完备性(柯西收敛准则)

数列收敛的充要条件是其为柯西列。
或者说:柯西列必收敛,收敛数列必为柯西列。
扩展资料
单调有界定理注意事项
1、单调有界定理只能用于证明数列极限的存在性,如何求极限需用其他方法;
2、数列从某一项开始单调有界的话,结论依然成立,这是因为增加或去掉数列有限项不改变数列的极限。
∨ 展开
热门推荐
猜你喜欢
-
 冰箱磁敏开关什么原理海尔冰箱磁敏开关位置 科学原理 2026-01-25
冰箱磁敏开关什么原理海尔冰箱磁敏开关位置 科学原理 2026-01-25 -
 立鸡蛋去邪祟竖鸡蛋叫魂是什么原理 科学原理 2026-01-25
立鸡蛋去邪祟竖鸡蛋叫魂是什么原理 科学原理 2026-01-25 -
 世界禁画雨中女郎恐怖,让人发疯发狂?原图恐怖原理 科学原理 2026-01-25
世界禁画雨中女郎恐怖,让人发疯发狂?原图恐怖原理 科学原理 2026-01-25 -
 液压分配阀液压分配阀工作原理图解 科学原理 2026-01-25
液压分配阀液压分配阀工作原理图解 科学原理 2026-01-25



 勾股定理现约有五百种证明方法,是数学定理中证明方法最多的定理之一
勾股定理现约有五百种证明方法,是数学定理中证明方法最多的定理之一
 立体几何的八个判定定理
立体几何的八个判定定理
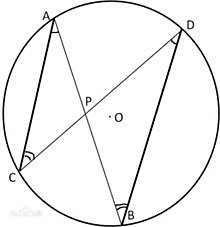 相交弦定理
相交弦定理
 贝叶斯定理
贝叶斯定理
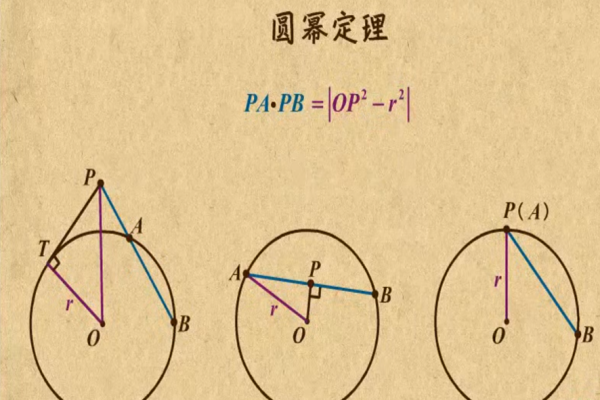 五大圆幂定理
五大圆幂定理
 惯性定理线性代数里的惯性定理
惯性定理线性代数里的惯性定理