【菜科解读】

五大圆幂定理如下：

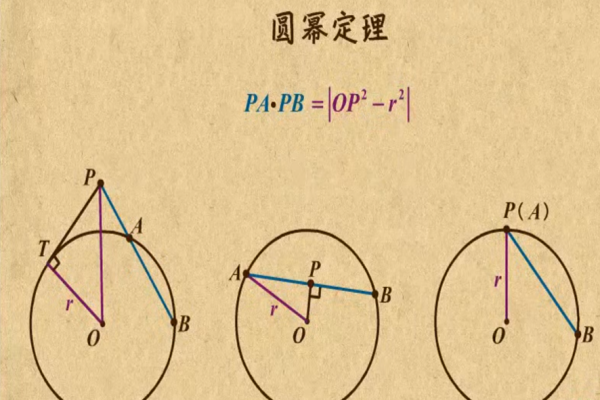
定理内容：过任意不在圆上的一点P引两条直线L1、L2，L1与圆交于A、B（可重合，即切线），L2与圆交于C、D（可重合，即切线），则有PA×PB=PC×PD 。

考虑经过P点与圆心O的直线，设PO交⊙O于M、N，R为圆的半径，则有PA×PB=PC×PD=PM×PN=(OP+R)│OP-R│=│OP²-R²│。

圆幂定理是一个总结性的定理，是对相交弦定理、切割线定理及割线定理（切割线定理推论）以及它们推论的统一与归纳。

根据两条与圆有相交关系的线的位置不同，有以下定理：

1、相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。

2、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

3、割线定理：从圆外一点P引两条割线与圆分别交于A、B；

C、D，则有PA·PB=PC·PD。

从上述定理可以看出，两条线的位置从内到外，都有着相似的结论。

经过总结和归纳，便得出了圆幂定理。

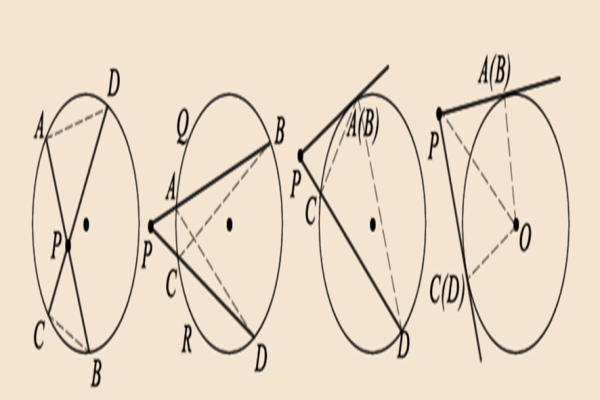
圆幂定理证明：

相交弦定理。

如图，AB、CD为圆O的两条任意弦。

相交于点P，连接AD、BC，由于∠B与∠D同为弧AC所对的圆周角，因此由圆周角定理知：∠B=∠D，同理∠A=∠C，所以 △PAD∽△PCB。

所以有：PA/PC=PD/PB，即：PA×PB=PC×PD 。

割线定理。

如图，连接AD、BC。

可知∠B=∠D，又因为∠P为公共角，所以有△PAD∽△PCB，同上证得 PA×PB=PC×PD。

切割线定理。

如图，连接AC、AD。

∠PAC为切线PA与弦AC组成的弦切角，因此有∠PAC=∠D，又因为∠P为公共角，所以有△PAC∽△PDA ，易证PA²=PC×PD。

PA、PC均为切线，则∠PAO=∠PCO=直角，在直角三角形中：OC=OA=R，PO为公共边，因此 △PAO≌△PCO。

所以PA=PC，所以 PA²=PC²。

综上可知，PA×PB=PC×PD 是普遍成立的。

证明完毕。